1.5 Rational Numbers¶
A rational number is defined to be a quotient 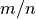 or
or
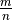 where
where 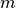 and
and 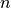 are integers.
are integers.
Note that 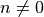 , because division by 0 is undefined. (We’ll talk
about dividing by zero in calculus a lot, along with the mysterious
infinity.)
, because division by 0 is undefined. (We’ll talk
about dividing by zero in calculus a lot, along with the mysterious
infinity.)
Decimal notation is just a rational number in disguise: 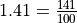 .
.
The meaning is simple: The bottom part (the denominator) tells you how many
equal parts a unit is divided into, and the top part (the numerator) tells
you how many of those parts you have. For instance, 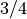 means you take
a whole unit, divide it into 4 equal parts, and take 3 of those parts.
means you take
a whole unit, divide it into 4 equal parts, and take 3 of those parts.
You can represent rational numbers on a number line, just like integers.
Negative rationals also appear on the number line – left of 0.
There is no unique way to represent rational numbers, which often confuses
students. 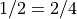 .
.
We need a way to see if two rationals are the same. We can use the rule for cross-multiplication.
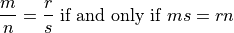
For instance:
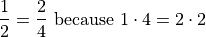
(This is convenient way to avoid factorizing or “simplifying” rationals.)
Note that integers are rationals – use a denominator of 1:
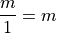
We can use cross-multiplication to solve simple equations:
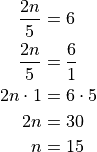
Note that, just like we have integers that add to zero, there are rationals that multiply to 1. These are called inverses. Mathematicians may debate about the proof of these numbers, but in this text, we assume that cross-multiplication works and derive the rest from this simple property.
We can factor out common factors in the numerator and the denominator. This is called the cancellation rule.
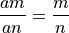
The proof is simple:
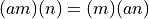
The rest of the proof is trivial.
Note that negative rationals can put their minus sign in three places.
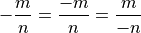
You can prove this with cross-multiplication as well.
With the cancellation rule, we can prove a curious property of rationals.
Suppose we have:
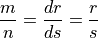
In practice, you can simplify rationals by finding common factors in the numerator and denominator.
Positive rationals are written with two positive integers (or two negative ones – you can cancel the factor of -1.) Negative rationals have two integers of opposite signs.
You can express all rationals in some unique lowest form. This is when the two integers share no common factors (besides 1, of course.)
Proof of this is in the text.
Adding two rationals is not trivial. (Multiplication is much easier.)
If they have a common denominator:
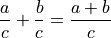
If they do not, or it is not immediately obvious how to obtain it, you can do general addition:
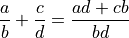
… TO BE CONTINUED …
Problem 7 d¶
Show that if 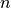 is a positive integer at most equal to
is a positive integer at most equal to 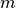 then:
then:
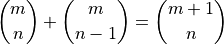
Hint 1¶
In order to solve this, we should first convert the binomial coefficients to ratios. Then we can try to add the left hand side, and finally, use cross multiplication to prove equality.
Hint 2¶
To add the two terms on the left hand side, either you can convert one or the other fraction so that they have the same denominator. Or, alternatively, just multiply the tops by the bottoms as in the general case for summing ratios.
Hint 3¶
Note that 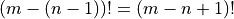 as the negative sign must distribute
to both
as the negative sign must distribute
to both 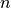 and
and 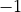 . This is a common mistake.
. This is a common mistake.
Hint 4¶
This may seem rather impossible, but remember that:
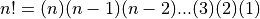
So it follows that:
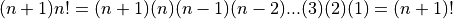
Note what we have done here. We have multiplied the factorial by the next highest integer, which means altogether, it is the next higher factorial.
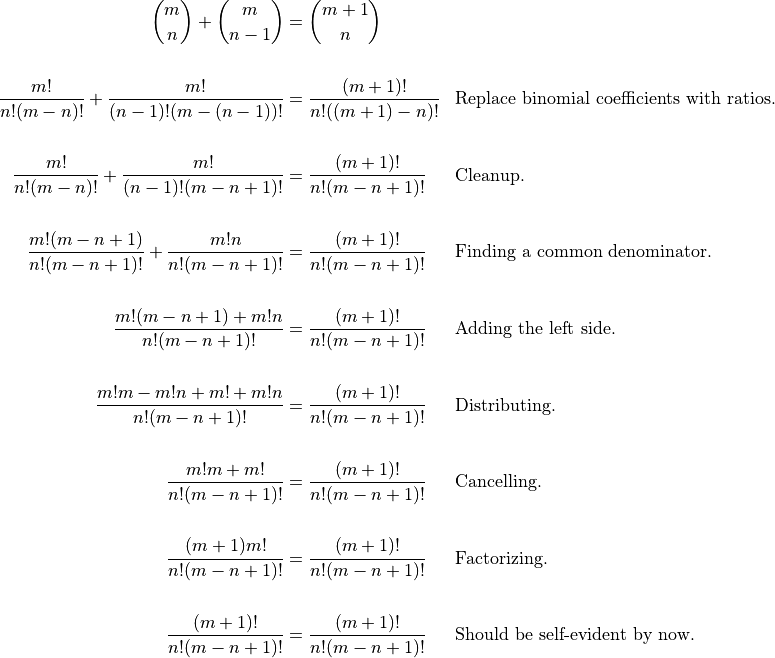
![\begin{aligned}
\binom{m}{n} + \binom{m}{n-1} &= \binom{m +1}{n} \\
\frac{m!}{n!(m-n)!} + \frac{m!}{(n-1)!(m-(n-1))!} &=
\frac{(m+1)!}{n!((m+1)-n)!} && \text{Replace binomial coefficients with
ratios.} \\
\frac{m!}{n!(m-n)!} + \frac{m!}{(n-1)!(m-n+1)!} &=
\frac{(m+1)!}{n!(m-n+1)!} && \text{Cleanup.} \\
\frac{m!(n-1)!(m-n+1)! + m!n!(m-n)!}{n!(m-n)!(n-1)!(m-n+1)!} &=
\frac{(m+1)!}{n!(m-n+1)!} && \text{General addition of ratios.} \\
[m!(n-1)!(m-n+1)! + m!n!(m-n)!]n!(m-n+1)! &=
(m+1)!n!(m-n)!(n-1)!(m-n+1)! && \text{Cross-multiplication.} \\
m!(n-1)!(m-n+1)! + m!n!(m-n)! &= (m+1)!(m-n)!(n-1)! && \text{Divide by } n!(m-n+1)!\text{.} \\
m!n!(m-n+1)! + m!n!(m-n)!n &= (m+1)!(m-n)!n! && \text{Multiply by } n\text{.} \\
m!(m-n+1)! + m!(m-n)!n &= (m+1)!(m-n)! && \text{Divide by } n!\text{.} \\
(m+1)!(m-n+1)! + (m+1)!(m-n)!n &= (m+1)!(m-n)!(m+1) && \text{Multiply by } m+1\text{.} \\
(m-n+1)! + (m-n)!n &= (m-n)!(m+1) && \text{Divide by } (m+1)!\text{.} \\
(m-n+1)!(m-n+1) + (m-n+1)!n &= (m-n+1)!(m+1) && \text{Multiply by } m-n+1\text{.} \\
m-n+1 + n &= m+1 && \text{Divide by } (m-n+1)!\text{.} \\
m+1 &= m+1 && \text{Cancel the }n\text{ and }-n\text{.}\\
\end{aligned}](../_images/math/69c3b584ce2b36fcec410051b128bb20d42b5ac8.png)

